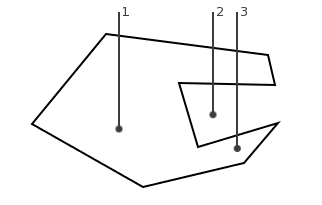
Point-in-polygon: Jordan Curve Theorem

From Sidvind

Calculating whenever a point is inside a polygon can sometimes be a hard and costly calculation. This article describes a quite cheap solution to calculate whenever a point is inside ANY closed polygon. In an open polygon it's hard to determine what's in and out so naturally it won't work.

A closed polygon with 3 points marked

The Jordan Curve Theorem states that a point is inside a polygon if the number of crossings from an arbitrary direction is odd. An image explains more than a thousand words so lets take a look at the picture. As you can see point 1 and 3 is inside the polygon but point 2 isn't. Follow the rays from each point and count each time you cross a line-segment. In this article I only deal with 2D polygons but it can easily used in a 3D-environment.

[edit] Find crossings

[edit] Casting a ray

One of the first things to do is to cast a ray from the point in an arbitrary direction. I use a ray along the Y axis (pointing upwards as in the picture) for simplicity. Along X-axis is good too, but use one of those or it gets a lot harder. Remember that I use the ray mentioned above throughout this article.

[edit] Finding the equation of a line-segment

As a first step, if the ray is along y-axis, check if the point x-coordinate is between the two points connecting the line. If not it don't cross it either. You can also check if the y-coordinate is above both points. The next step is to find the equation of the line. Hopefully you remember this from grade school. The equation of a straight line is (Swedish notation). The slope is and offset is . Do the math we have the equation. Now, insert the x-coordinate of the point into the equation. If the result is larger than the y-coordinate the ray does not cross the line-segment.

Repeat this for each line-segment.

[edit] C/C++ implementation

/* The points creating the polygon. */
float x[8];
float y[8];
float x1,x2;

/* The coordinates of the point */
float px, py;

/* How many times the ray crosses a line-segment */
int crossings = 0;

/* Coordinates of the points */
x[0] = 100;	y[0] = 100;
x[1] = 200;	y[1] = 200;
x[2] = 300;	y[2] = 200;
x[3] = 300;	y[3] = 170;
x[4] = 240;	y[4] = 170;
x[5] = 240;	y[5] = 90;
x[6] = 330;	y[6] = 140;
x[7] = 270;	y[7] = 30;

/* Iterate through each line */
for ( int i = 0; i < 8; i++ ){
	
	/* This is done to ensure that we get the same result when
	   the line goes from left to right and right to left */
	if ( x[i] < x[ (i+1)%8 ] ){
		x1 = x[i];
		x2 = x[(i+1)%8];
	} else {
		x1 = x[(i+1)%8];
		x2 = x[i];
	}
	
	/* First check if the ray is possible to cross the line */
	if ( px > x1 && px <= x2 && ( py < y[i] || py <= y[(i+1)%8] ) ) {
		static const float eps = 0.000001;

		/* Calculate the equation of the line */
		float dx = x[(i+1)%8] - x[i];
		float dy = y[(i+1)%8] - y[i];
		float k;

		if ( fabs(dx) < eps ){
			k = INFINITY;	// math.h
		} else {
			k = dy/dx;
		}

		float m = y[i] - k * x[i];
		
		/* Find if the ray crosses the line */
		float y2 = k * px + m;
		if ( py <= y2 ){
			crossings++;
		}
	}
}

printf("The point is crossing %d lines", crossings);
if ( crossings % 2 == 1 ){
	printf(" thus it is inside the polygon");
}
printf("\n");